Rata-rata Aritmetik dan Geometrik

Kasus Kinerja Berurutan

Kinerja investasi seseorang dengan modal awal Rp100 juta punya sejarah pertumbuhan seperti di bawah:

• Tahun ke-1: 30%
• Tahun ke-2: -25%
• Tahun ke-3: 40%

Berapakah rata-rata produksi pabrik itu?

Menghitung Pakai Rerata (Rata-rata) Aritmetik

Rata-rata aritmatik:
= ( 30% + -25% + 40% ) ÷ 3
= 45% ÷ 3 = 15%

Rumus di atas adalah rerata aritmetik. Kinerja investasi dinyatakan tumbuh rata-rata 15% per tahun.

Rerata ini punya karakteristik:

• Mudah dihitung
• Familiar
• Cocok untuk data yang independen, misal: persentase ujian satu siswa tidak ada pengaruh dengan hasil siswa lain

Problem kita di atas adalah rangkaian kejadian yang terkait antara satu tahun dan tahun berikutnya. Mengatakan kinerja tumbuh 15% bisa salah. Angkanya bisa terlalu besar.

Dengan memakai asumsi rata-rata aritmetik, maka kalkulasinya kinerja akhirnya: 100 × 115% × 115% × 115% = 152 juta. Angkanya terlalu besar.

Kalkulasi yang benar seharusnya: 100 * 130% * 75% * 140% = 136,5, ini adalah kinerja akhir investor tersebut.

Rata-rata (Rerata) Geometrik

Rumus Rerata Geometrik:

= ( ( 1 + Rerata1 ) x ( 1 + Rerata2 ) x ( 1 + RerataN ) ) ^ ( 1 ÷ N ) - 1
= ( ( 130% ) x ( 75% ) x ( 140% ) ^ ( 1 ÷ 3 ) - 1
= 9,07%

Rerata geometrik menghitung faktor pertumbuhan majemuk karena terjadinya perkalian antar periode. Rerata geometrik juga disebut rata-rata diperhalus, karena menghasilkan asumsi pertumbuhan stabil.

Dalam diskusi finansial rerata geometrik juga sering disebut compounded annual growth rate (CAGR), biasanya disingkat dalam “YoY” menilik sifatnya, atau “disetahunkan” (annualized). Rerata geometrik kadang disebut juga time-weighted rate of return.

Rerata geometric atau CAGR umumnya melaporkan angka persentase lebih kecil dibanding rerata aritmetik atau rata-rata biasa.

Plus/Minus Rerata Geometrik

• Rumit kalkulasinya:
  • Rumus: (1+akumulasi)^(1/N)-1
  • RUmus: (awal/akhir)^(1/N)-1
• Perlu kalkulator pangkat N—di mana N adalah jumlah periode
• Disebut juga Compounded Annual Growth Rate (CAGR) atau time weighted rate of return.
• Dinotasikan dalam “% YoY” (jangka panjang) atau “disetahunkan” (annualised)
• Untuk even berkelanjutan/majemuk, seperti hasil portofolio investasi yang terus diinvestasikan setelahnya
• Menghaluskan pertumbuhan agar mudah dibaca
• Untuk komparasi antar aset investasi, acuan (benchmark) indeks, dan kinerja investasi lainnya

Baca juga: Formula CAGR

Aplikasi Geometric Mean?

Dalam berbagai persoalan investasi dan keuangan, sangat dianjurkan membandingkan dengan rerata geometrik. Kalkulasi finansial dan investasi biasanya berhubungan dengan pertumbuhan majemuk. Lihatlah contoh di atas, ada selisih yang lumayan antara kalkulasi rata-rata aritmetik dan geometrik. Semakin besar persentase dan jumlah waktunya, hasil kalkulasi bisa makin berbeda.

Pertumbuhan majemuk itu seperti seseorang mengelola dana dari awal 100, ditumbuhkan lagi, ditumbuhkan lagi.

Contoh pemakaian perbandingan rerata geometrik 10 tahunan berikut:

• Risiko inflasi: 4% (misal aja)
• Portofolio investasi: 6%
• IHSG 2011-2021: 4,75%

Dari bacaan rerata geometriknya, kita memahami bahwa bahwa portofolio investasi dan IHSG itu semua sudah cukup mengalahkan inflasi. Yang IHSG itu setara akumulasi 59,12%, dari 26 Ags 2011 hingga sekarang 6112 ya guys.

Kinerja IHSG Selama 23 Tahun Terakhir

Contoh aplikasi rerata geometrik adalah mengkalkulasikan kinerja total IHSG selama 23 tahun terakhir.

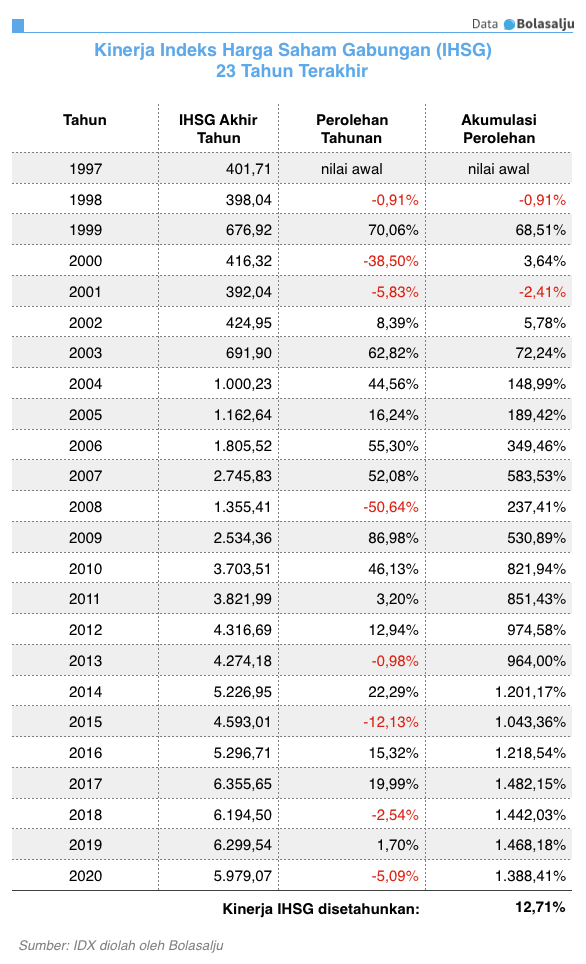
Dalam indeks tersebut terekam kinerja saham seluruh konstituen yang ada di IHSG setiap tahunnya, termasuk dari dividen. Dari pertumbuhan tiap tahun, ada saham yang naik, ada yang turun, ada yang bubar, ada yang terus berjaya. Semua kinerja ditotal lalu terbentuklah indeks tahunan. Dari hasil tahun demi tahun perusahaan-perusahaan itu tumbuh.

Dari kalkulasi di atas, kita baca perusahaan-perusahaan di IHSG telah menghasilkan perolehan total 1.388,41% selama 23 tahun atau 12,71% YoY (disetahunkan).

Nah… sekarang jadi tahu kan kegunaan rerata geometrik.